Gửi mọi người tham khảo một phương pháp tính pi (trong nội dung chương trình môn Phương pháp tính)
Link download: https://drive.google.com/file/d/0BzfH_xfr9rprWUNpbFF1UFhSZkU/view?usp=sharing
Thứ Năm, 28 tháng 5, 2015
Thứ Sáu, 8 tháng 5, 2015
Một phương pháp tính e với sai số cho trước - phương pháp tính
Thứ Ba, 5 tháng 5, 2015
Nội dung trọng tâm môn phương pháp tính
Nội dung môn phương pháp tính gồm các phần chính như sau:
1. Xác định dạng biểu diễn của đa thức
2. Phép nội suy và áp dụng
3. Tính gần đúng giá trị hàm sơ cấp
4. Tính gần đúng nghiệm của phương trình đại số.
Các
tài liệu của nhóm đi kèm 4 chủ đề trên (tương đối) đính kèm như sau.
Mọi người nắm ý chính và sau đó vô thi tính toán tương tự.
Lưu ý: đây là quan điểm cá nhân chứ ko phải thầy dặn dò gì cả, nên chỉ mang tính tham khảo thôi nhé.Link download:
Link 1 hoặc Link 2
Thứ Sáu, 1 tháng 5, 2015
Chủ Nhật, 5 tháng 4, 2015
Thứ Năm, 2 tháng 4, 2015
Đường thẳng Simson, Đường thẳng Steiner
1. Định lý về Đường thẳng Simson
Cho tam giác nội tiếp trong đường tròn tâm
nội tiếp trong đường tròn tâm 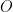 . Gỉa sử
. Gỉa sử  là một điểm nằm trên
là một điểm nằm trên 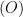 sao cho
sao cho  không trùng với ba đỉnh của tam giác. Khi đó hình chiều vuông góc
không trùng với ba đỉnh của tam giác. Khi đó hình chiều vuông góc  của
của  lần lượt trên
lần lượt trên 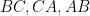 cùng nằm trên một đường thẳng. (Đường thẳng này gọi là đường thẳng
cùng nằm trên một đường thẳng. (Đường thẳng này gọi là đường thẳng 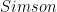 của điểm
của điểm  đối với tam giác
đối với tam giác  )
)
Chứng minh :
Ta có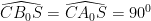 , suy ra tứ giác
, suy ra tứ giác 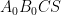 nội tiếp, suy ra
nội tiếp, suy ra  . Mặt khác vì
. Mặt khác vì 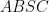 nội tiếp nên
nội tiếp nên  .
.
Nhưng vì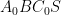 là tứ giác nội tiếp (
là tứ giác nội tiếp (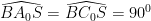 ) nên
) nên  .
.
Vậy cùng thuộc một đường thẳng.
cùng thuộc một đường thẳng.
2. Định lí về đường thẳng Steiner :
Cho tam giác nội tiếp đường tròn tâm
nội tiếp đường tròn tâm 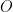 , điểm
, điểm  bất kì thuộc đường tròn sao cho
bất kì thuộc đường tròn sao cho  không trùng với các đỉnh của tam giác. Gọi
không trùng với các đỉnh của tam giác. Gọi 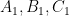 lần lượt là điểm đối xứng với
lần lượt là điểm đối xứng với  qua các đường thẳng
qua các đường thẳng 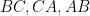 . Khi đó ba điểm
. Khi đó ba điểm 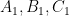 và trực tâm
và trực tâm  của tam giác
của tam giác  cùng nằm trên một đường thẳng (Đường thẳng này là đường thẳng
cùng nằm trên một đường thẳng (Đường thẳng này là đường thẳng 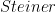 của điểm
của điểm  đối với tam giác
đối với tam giác  .
.
Chứng minh:
Dễ dàng thấy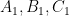 cùng nằm trên một đường thẳng song song với đường thẳng
cùng nằm trên một đường thẳng song song với đường thẳng 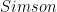 của điểm
của điểm  đối với tam giác
đối với tam giác  .
.
Ta có mà
mà 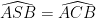 nên
nên  , suy ra
, suy ra 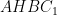 là tứ giác nội tiếp.
là tứ giác nội tiếp.
Từ đó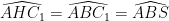
Hoàn toàn tương tự, tứ giác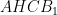 nội tiếp nên
nội tiếp nên 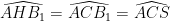
Lại có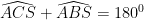 (tứ giác
(tứ giác 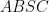 nội tiếp)
nội tiếp)
Do đó , suy ra
, suy ra 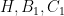 thẳng hàng.
thẳng hàng.
Vậy : cùng thuộc một đường thẳng.
cùng thuộc một đường thẳng.
Cho tam giác
Chứng minh :
Ta có
Nhưng vì
Vậy
2. Định lí về đường thẳng Steiner :
Cho tam giác
Chứng minh:
Dễ dàng thấy
Ta có
Từ đó
Hoàn toàn tương tự, tứ giác
Lại có
Do đó
Vậy :
Đăng ký:
Nhận xét (Atom)











.png)


